1. 朴素贝叶斯的介绍与应用
1.1 朴素贝叶斯的介绍
朴素贝叶斯算法(Naive Bayes, NB)是应用最为广泛的分类算法之一。它是基于贝叶斯定义和特征条件独立假设的分类方法。由于朴素贝叶斯法基于贝叶斯公式计算得到,有着坚实的数学基础,以及稳定的分类效率。NB模型所需估计的参数很少,对缺失数据不太敏感,算法也比较简单。当年的垃圾邮件分类都是基于朴素贝叶斯分类器识别的。
什么是条件概率,我们从一个摸球的例子来理解。我们有两个桶:灰色桶和绿色桶,一共有7个小球,4个蓝色和3个紫色,分布如下图:
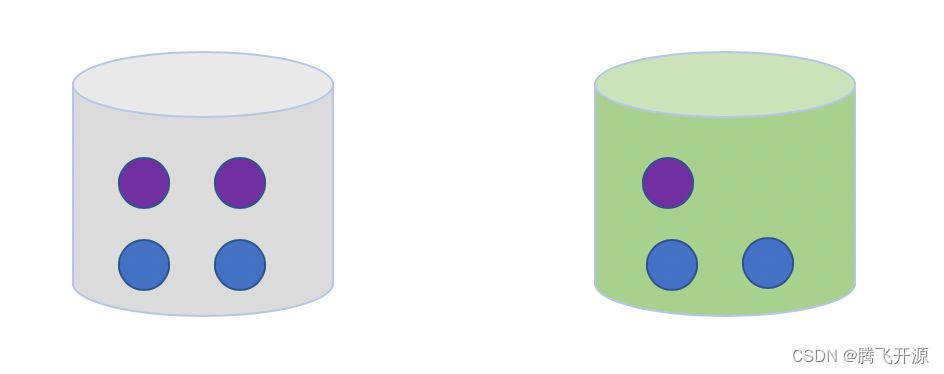
从这7个球中,随机选择1个球是紫色的概率p是多少?选择过程如下:
- 先选择桶
- 再从选择的桶中选择一个球
p ( 球 = 紫色 ) = p ( 选择桶 ) ∗ p ( 从灰桶中选择紫色 ) + p ( 选择绿桶 ) ∗ p ( 从绿桶中选择紫色 ) = 1 2 ∗ 2 4 + 1 2 ∗ 1 3 p(球 = 紫色)=p(选择桶) * p(从灰桶中选择紫色)+p(选择绿桶)*p(从绿桶中选择紫色)=\frac{1}{2}*\frac{2}{4}+\frac{1}{2}*\frac{1}{3} p(球=紫色)=p(选择桶)∗p(从灰桶中选择紫色)+p(选择绿桶)∗p(从绿桶中选择紫色)=21∗42+21∗31
上述我们选择小球的过程就是条件概率的过程,在选择桶的颜色的情况下是紫色的概率,另一种计算条件概率的方法是贝叶斯准则。
贝叶斯公式是英国数学家提出的一个数据公式:
p ( A ∣ B ) = p ( A , B ) p ( B ) = p ( B ∣ A ) ∗ p ( A ) ∑ a ∈ ℑ A p ( B ∣ a ) ∗ p ( a ) p(A|B)=\frac{p(A,B)}{p(B)}=\frac{p(B|A)*p(A)}{\sum_{a\in\Im_{A}}p(B|a)*p(a)} p(A∣B)=p(B)p(A,B)=∑a∈ℑAp(B∣a)∗p(a)p(B∣A)∗p(A)
p ( A , B ) : p(A,B): p(A,B): 表示事件A和事件B同时发生的概率。
p ( B ) : p(B): p(B): 表示事件B发生的概率,叫做先验概率; p ( A ) : p(A): p(A): 表示事件A发生的概率。
p ( A ∣ B ) : p(A|B): p(A∣B): 表示当事件B发生的条件下,事件A发生的概率叫做后验概率。
我们用一句话理解贝叶斯:世间很多事都存在某种联系,假设事件A和事件B。人们常常使用已经发生的某个事件去推断我们想要知道的之间的概率。例如,医生在确诊的时候,会根据病人的舌苔、心跳等来判断病人得了什么病。对病人来说,只会关注得了什么并病,医生会通过已经发生的事件来确诊具体的情况。这里就用到了贝叶斯思想,A是已经发生的病人症状,在A发生的条件下是B_i的概率。
1.2 朴素贝叶斯的应用
朴素贝叶斯算法假设所有特征的出现相互独立互不影响,每一特征同等重要,又因为其简单,而且具有很好的可解释性。一般相对于其他精心设计的更复杂的分类算法,朴素贝叶斯分类算法是学习效率和分类效果较好的分类器之一。朴素贝叶斯算法一般应用在文本分类,垃圾邮件的分类,信用评估,钓鱼网站检测等。
2. 贝叶斯分类算法实践
2.1 鸢尾花数据集
2.1.1 库函数导入
import warnings
warnings.filterwarnings('ignore')
import numpy as np
# 加载鸢尾花数据集
from sklearn import datasets
# 导入高斯朴素贝叶斯分类器
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
2.1.2 数据导入&分析
X, y = datasets.load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
我们需要计算两个概率分别是:条件概率: P ( X ( i ) = x i ∣ Y = c k ) P(X^{(i)}=x^{i}|Y=c_k) P(X(i)=xi∣Y=ck) 和类目 c k c_k ck 的先验概率: P ( Y = c k ) P(Y=c_k) P(Y=ck)。
通过分析发现训练数据是数值类型的数据,这里假设每个特征服从高斯分布,因此我们选择高斯朴素贝叶斯来进行分类计算。
2.1.3 模型训练
# 使用高斯朴素贝叶斯进行计算
clf = GaussianNB(var_smoothing=1e-8)
clf.fit(X_train, y_train)
GaussianNB(var_smoothing=1e-08)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
GaussianNB(var_smoothing=1e-08)
2.1.4 模型评估和预测
# 评估
y_pred= clf.predict(X_test)
acc = np.sum(y_test == y_pred) / X_test.shape[0]
print("Test Acc :%.3f" % acc)
# 预测
y_proda = clf.predict_proba(X_test[:1])
print(clf.predict(X_test[:1]))
print("预计的概率值:", y_proda)
Test Acc :0.967
[2]
预计的概率值: [[1.63542393e-232 2.18880483e-006 9.99997811e-001]]
2.1.5 原理简析
高斯朴素贝叶斯假设每个特征都服从高斯分布,我们把一个随机变量X服从数学期望为μ,方差为σ2的数据分布称为高斯分布。对于每个特征我们一般使用平均值来估计μ和使用所有特征的方差估计σ2。
P ( X ( i ) = x ( i ) ∣ Y = c k ) = 1 2 π σ y 2 e x p ( − ( x ( i ) − μ c k ) 2 2 σ c k 2 ) P(X^{(i)}=x^{(i)}|Y=c_k)=\frac{1}{\sqrt{2\pi\sigma_{y}^{2}}}exp(-\frac{(x^{(i)}-\mu_{c_k})^{2}}{2\sigma_{c_k}^{2}}) P(X(i)=x(i)∣Y=ck)=2πσ